How to Calculate Compound Interest in Excel

If you find yourself wondering how to calculate compound interest in Excel, you've come to the right place. Compound interest has many uses – it's one of the key features that consumers look for when building their savings profile; it helps you understand loans and can determine where you should invest your hard-earned money.

If you learn how compound interest works and how to calculate compound interest in Excel independently, you can make better decisions about your investment plan.

What is compound interest?

Compound interest is the interest earned from an investment based on both the initial deposit and the accumulated interest over time. In simple words, compound interest is the interest earned on interest. 

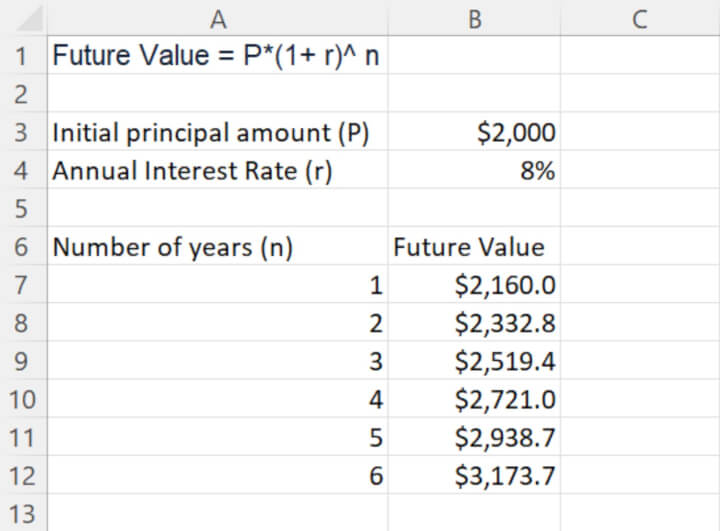
For example, you invest $2,000 with an 8% annual interest rate compounded annually. A year after, you earn $160 in interest from the initial deposit ($2,000 x 0.08), so your total investment is valued at $2,160 ($2,000 in initial deposit + $160 in interest). At the end of the second year, you will have $2,332.8 ($2,160 in initial deposit + $172.8 in interest). And so on. 

With compound interest, the investment grows further as the interest accumulates, and the initial deposit grows bigger by also considering the interest earned previously. 

How to calculate compound interest in Excel

Compound interest is calculated by multiplying the initial principal amount by one plus the annual interest rate, raised to the number of compound periods, or simply put, the formula below:

Future Value = P* (1+ r)^ n

P = the initial principal amount deposited, 

r = annual interest rate (expressed as a decimal)

n = the number of compound periods (in other words, the number of years)

Using the previous example, the future value of the investment after two years can be calculated by following the formula of Future Value = P*(1+ r)^ n

= $2,000 x (1+0.08)^2

= $2,332.8

Compound interest formula using relative cell reference in Excel

By using relative cell reference, we will be able to calculate compound interest in a more effective and efficient fashion compared to the manual calculation.

Begin by simply inputting all relevant data into an Excel Spreadsheet. 

Then, to calculate the future value, enter the formula by referencing the values in cells B3, B4, and B5.

The formula returns the same value = $2,332.8, as seen previously. 

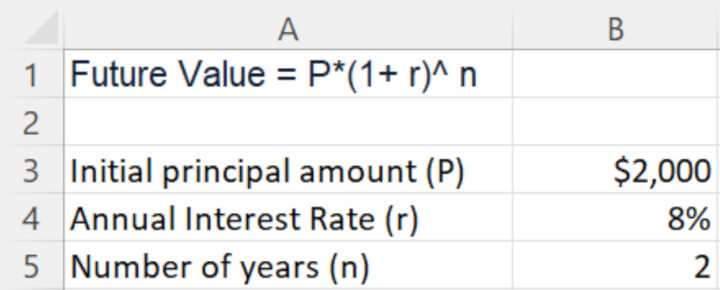
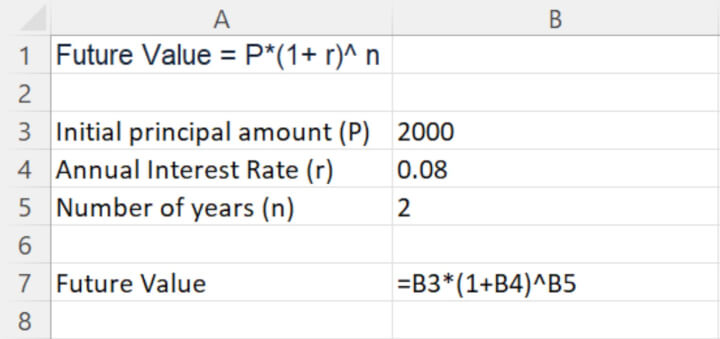
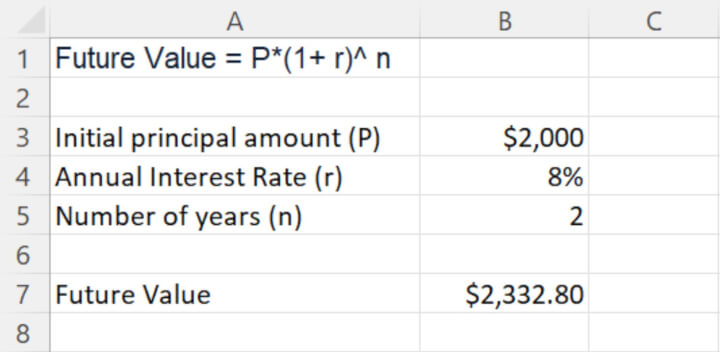
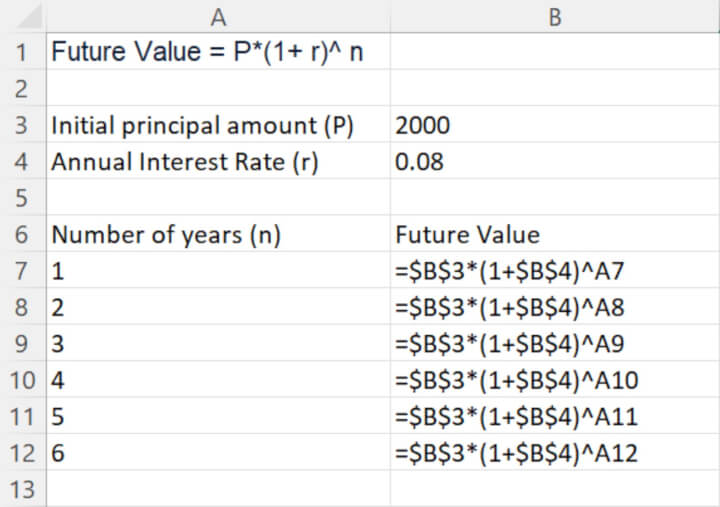
Calculate compound interest over multiple years in Excel

When evaluating different investment plans, consumers often refer to the future value over multiple years to determine the best return on their initial principal over time. 

To calculate compound interest over multiple years in Excel, we can use the same formula but with slightly different formatting to have an overall continuous view of the yearly progression on our regular deposit.

Just like what we have just done, input the formula for referencing the corresponding cells in cell B7. 

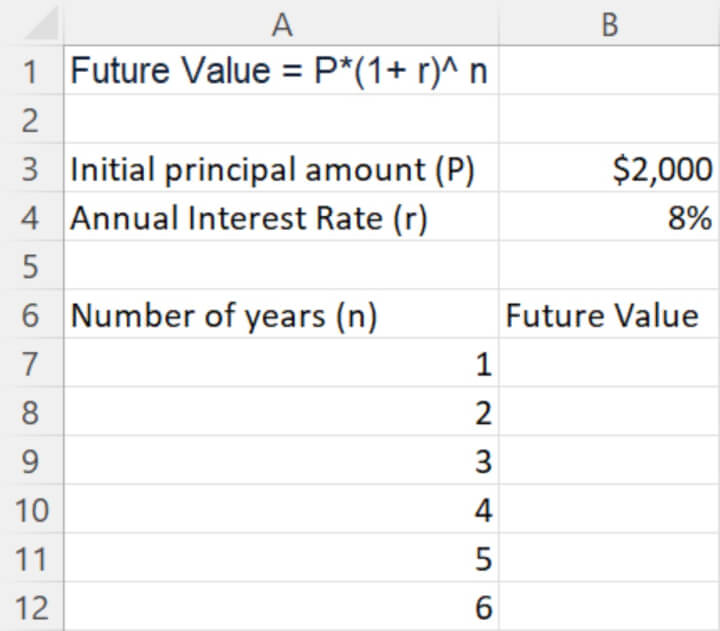
Then, since the only variable is the no. of compound periods, and with the cell reference for the initial principal amount (P) and annual interest rate (r) remain the same, be sure to “lock” it by putting a dollar sign before the cell and column references when copying the formula down from cell B7 to cell B12. This is an example of absolute reference. 

These formulas will return these values: 

Calculate future value when interest is paid monthly or quarterly in Excel

In some scenarios, the interest of the investment plan is paid monthly or quarterly. When the interest is compounded on a monthly basis, the future value returns a higher value compared to a quarterly compounded interest plan. The more frequently the interest is paid out, the higher value it returns. And the longer the investment is, the more compounded interest is earned on interest.

(a) Interest is compounded monthly

When the interest is paid monthly, the frequency of the interest payout is 12 times a year. The formula becomes: 

Future Value = P* (1+ r/12)^ (n*12)

The annual interest rate (r) is divided by 12, because the interest payout is compounded on a monthly basis, the no. of compound periods (n) is multiplied by 12 to calculate the number of months in the no. of years over which the investment is made. 

In Excel, set up the formula like below by including cell B6, the compounding period - 12 by using relative cell reference. 

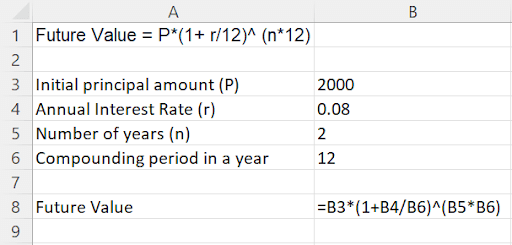
If the interest is compounded monthly, the future value returns $2,345.78 after 2 years.

(b) Interest is compounded quarterly

When the interest is paid quarterly, the frequency of the interest payout is four times a year. The formula becomes: 

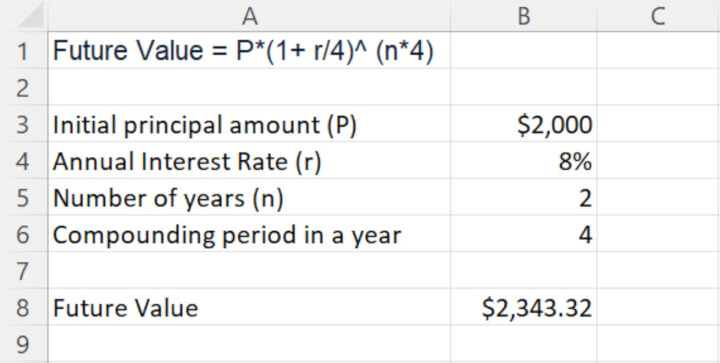
Future Value = P* (1+ r/4)^ (n*4)

The annual interest rate (r) is divided by four because the interest payout is compounded on a monthly basis. The no. of compound periods (n) is multiplied by 4 to calculate the number of months in the number of years over which the investment is made. 

Using the same setup as above, to calculate the future value when the interest is compounded quarterly, simply change the compounding period in a year from 12 to 4. 

The formula remains the same, as indicated in cell B8.

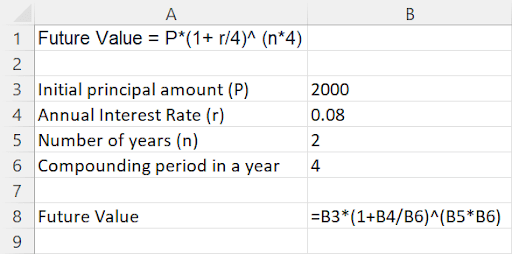
If the interest is compounded quarterly, the future value returns $2,343.32 after two years. 

Future value compound interest formula in Excel

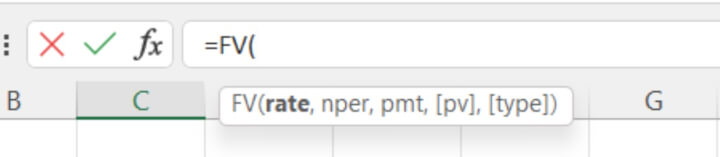
In fact, Excel has a built-in financial function - FV function - which is designed to return the future value of an investment based on the values of a few variables.

Begin by inputting = FV in the formula bar, and you will see the values required to compute a future value.

Before we look into what the arguments refer to in the FV formula, let’s create the FV formula by using the previous example of calculating monthly compounded interest. 

The value returns $2,345.78, same as what we have seen previously.

There are five arguments in the FV excel formula:

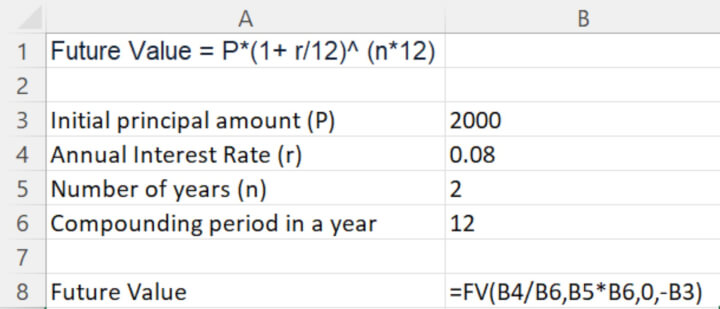
• rate refers to Interest rate of each period; 
  • In the example: r/12 or 8%/12, as it’s compounded monthly, expressed as B4/B6
• nper refers to number of payment periods
  • In the example: n*12 or 2*12, as the interest is paid out monthly, and the investment plan is for 2 years, expressed as B5*B6
• pmt refers to additional payment or deposit per period
  • In the example: 0, as there’s no additional payment or deposit,
• pv refers to the present value or the initial principal amount P, it is expressed as an negative value
  • In the example: $2,000 is the initial principal amount P, expressed as -B3
• type refer to the timing of when the additional deposits or payments are due, 0 when it is due at the end of the period and 1 at the start of the period; it’s an optional argument
  • In the example: such argument is not available, it’s omitted. 

Knowing how to calculate compound interest is crucial when evaluating different investment options and their performances. Excel makes it easy and simple to do so. Check out the other helpful resources on how to use Excel formulas to get ahead of the game!

Level up your Excel skills

Become a certified Excel ninja with GoSkills bite-sized courses

Start free trial